Creating behavioral models for non-linear dynamical systems, and especially RF devices, is a challenging task. Most approaches require a substantial prior knowledge of the physical structure in order to be able to generate suitable mathematical models for the desired characteristics. However, since it is usually not attractive for manufacturers to pass on extensive knowledge about internal components to third parties, one has to rely mainly on black- or gray-box models. An approach is to fit a parameterized model based on representative measurement data, following the example of the Hammerstein-Wiener models. In order to integrate new devices into the Cadence AWR Design Environment at MATLAB toolbox has been created to fit SISO and MIMO Hammerstein-Wiener models to given measurement data. These models feature the following discrete structure

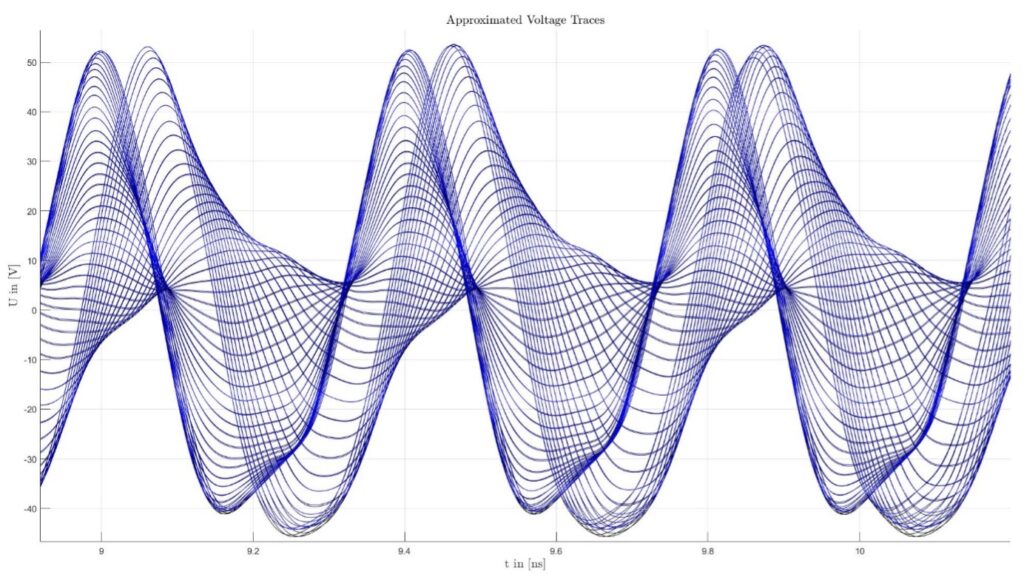
Where f_1(u_t) represents an arbitrary input nonlinearity, G(q) is a linear dynamical system similar to e.g. digital filters with the delay operator q and f_2(w_t) is an arbitrary output nonlinearity. Within this toolbox several modelling approaches for f_1 and f_2 have been implemented such as cubic and B-splines or simple polynomial models. The linear dynamical system G is currently implemented utilising autoregression models with exogenous input (ARX) models. A decisive advantage of this approach, is the fitting process, where only simple linear least squares problems have to be solved and special structures encourage the use of efficient solution methods. In addition, the generalizability of the model for applications in RF Devices plays a major role. It has been shown that Hammerstein-Wiener models have excellent properties when the model parameters are carefully selected. As an example, the voltage characteristics at the output port (black) of a Ga-FET for a frequency sweep of two-tone signals at the input port are given here. The corresponding Hammerstein-Wiener model (blue) was only generated with a single two-tone signal, but nevertheless provides sufficiently exact results for all other cases.